Na fotografía vese a
Conca do río Miño cuns datos que me interesan para o
comentario que ven a continuación.
----------------
Escribe Secundino Lorenzo.
Autor da web "O pai Miño".
O nº Pi e a lonxitude do río
Miño.
O número de Stolom é unha
aproximación de ¶ no caso do río Miño
Todo o mundo coñece o número
PI, sabe do seu valor pola escola, daquela tomábamos 3,14 como o
valor aproximado deste número, tamén se sabe que é a relación que
existe entre a lonxitude dunha circunferencia e o diámetro. A famosa
fórmula L = 2 ¶ r que permitía calcular a lonxitude L da
circunferencia multiplicando ¶ por 2 r ou sexa polo diámetro.
O que moitos non saben é que
o número pi en realidade , é un número con infinitas cifras decimais non periódicas, ou sexa non se repiten nunca; o que os
matemáticos chamamos un número irracional.
Hai miles de cifras decimais
calculadas do número ¶ , entre elas 3,141592653...
Fai uns días o 14 de marzo
celebrouse o día de ¶
xa que según a notación
anglosaxona no mes 3 (marzo), o día 14, do ano 15 as 9 horas, 26
minutos e 53 segundos era unha das moitas aproximacións de pi .
Pois ben, hai moitos
resultados sorprendentes nos que aparece este número fascinante,
algúns que deixan asombrados a primeira de cambio e de eso trata
este pequeno artículo.
Hans Henrik Stolum é un
xeólogo da Universidade de Cambridge (Reino Unido) que en 1996,
chegou a seguinte conclusión:
"A relación
entre o doble da lonxitude dun río e a distancia en liña
recta entre o nacemento e a desembocadura e un número
moi aproximado a pi"
Nota: moi próximo a pi en ríos
grandes e sinuosos e con números menores pero próximos si o
río vai entre montañas ou canóns...
O resultado
é moi interesante e dende logo sorprendente.
Dende o meu
punto de vista é máis sorprendente inda xa que
inmediatamente veñen dous pensamentos que hai que
comprobar ou polo menos interesarse:
1.- Que pasos seguiu
Hans-Henrik Stolum para chegar a esta conclusión?.
2.- Será certa para
o río Miño?.
1.1.-Sobre a primeira parte
decir que as teorías de Hans-Henrik Stolum aparecen no seu libro "River
Meandering as a Self-Organization Process"
, publicado en 1996,
ver este link. Polo medio está a
"Teoría do caos",
onde pequenas fluctuacións, nas condicións iniciais, levan a
resultados cuantificables no tempo, e datos determinables.
Por suposto a teoría escapa a este pequeno traballo que pretende
únicamente a divulgación do feito.
Podedes ver este
link con algúns detalles.
Tamén este pdf.
De tódolos xeitos non é dificil interpretar
uns cálculos que deixan ver, xeneralizando ,
como o número pi está presente.
Ver
esta interpretación.
A idea está tomada desta paxina:
"sobre todo matemáticas de las buenas,
bonitas y baratas".
2.1 Sobre a comprobación no caso do río Miño, ten os datos seguintes:
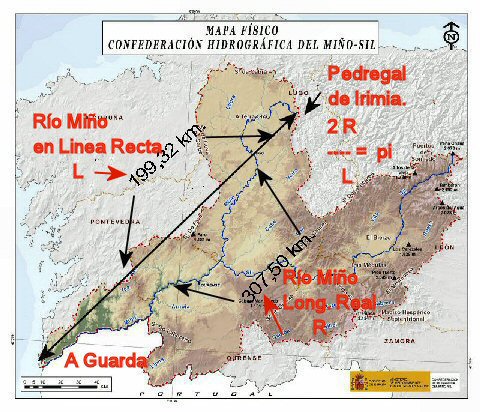
Lonxitude do río Miño : 307,5 km.
("D.X. Dicionario
Xeográfico Ilustrado
de Galicia". 2009. Editado por Xeogal Publicacións,
S.L. e que entre outros moitos autores ten a Fco. Javier Río Barja.
)
Lonxitude en liña recta, dende o Pedregal de Irimia ata a
desembocadura na Guardia : 199,5 km. ( Datos medidos
directamente co aplicativo Google Earth, opción rutas).
Cálculo do
número de Stolom = 2 x 307,5 / 199,5 = 3,083
Diferencia
con ¶, redondeando, 3,141593-3,082707 =0,06
Podemos dar o número de Stolom como unha boa aproximación
de pi.
Dito doutro xeito que poda sorprender máis: a lonxitude real
do río Miño é, aproximadamente:
¶/2 veces
a lonxitude en liña recta dende o nacemento ata a desembocadura.
Ou sexa si a lonxitude real
dun río a chamamos R, e a lonxitude en liña recta a chamamos L
resulta que:
Con esta
fórmula calculamos a lonxitude real dun río, sabendo
a lonxitude en linea recta:
R =
¶/2
. L
Neste caso no
río Miño sae unha lonxitude de 313,17 km., soio 6 km. de diferencia,
non está mal...
Sorprende ou
non ?
 Saír á río Miño
Saír á río Miño
 Salir al río Miño
Salir al río Miño
Cálculos de
interpretación.
A mediados da década de 1990 o
geólogo Hans-Henrik Stolum, da
Universidade de Cambridge , observou que a relación
entre o doble da lonxitude dun río e a distancia en
líña recta dende o seu nacemento ata a
desembocadura é, xeralmente, un valor próximo a 3.
Observou: que nos ríos máis
antigos, que tuveron a oportunidade de desenrolar
cursos longos e con moitos meandros, a relación
acércase a π (3,141592...) e normalmente este
número é rabasado no caso de meandros moi pechados.
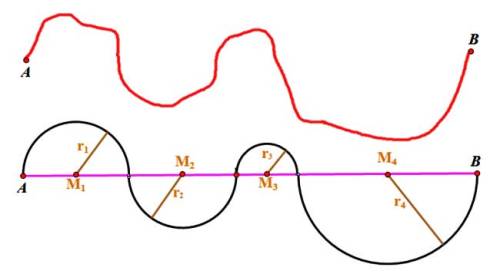
A idea é a seguinte: na primeira
imaxen aparece un río e na segunda a súa
"modelización matemática" con semicircunferencias...
A lonxitude do
río de A a B, será a suma das
lonxitudes das semicircunferencias
π r1 + π r2
+ π r3 + π r4
e a
distancia lineal entre A e B a suma
dos diámetros
2 r1 + 2 r2
+ 2 r3 + 2 r4
polo que a razón
entre o doble da lonxitude e a
distancia líneal será
2 x (π r1 + π r2
+ π r3 + π r4)
/ (2 r1 + 2 r2
+ 2 r3 + 2 r4)
= π
A
vista deste resultado parece lóxico
pensar na súa xeneralización e
fundamentación, inda que polo menos,
poda verse fundamentado neste
exemplo.